Każdy analityk wykonujący chromatografię kolumnową spotyka się z pojęciem półek teoretycznych. To parametr wiele mówiący o kolumnie chromatograficznej, jej kondycji. Jeśli przeczytałeś „Wstęp do HPLC” wiesz, że kolumna chromatograficzna nie zawiera żadnych półek. Czym więc są półki teoretyczne i jak wpływają na rozdział? Tego dowiesz się w tym artykule.
Gra o Rozdzielczość
W chromatografii naszym świętym Graalem jest rozdzielczość (Rs). To parametr, który mówi nam, czy dwa składniki mieszaniny opuściły kolumnę osobno, czy też zlały się w jeden nieczytelny sygnał.
Na rozdzielczość wpływają trzy czynniki: retencja (jak długo substancje zostają na kolumnie), selektywność (jak bardzo „lubią” fazę stacjonarną względem siebie) oraz wydajność. To właśnie wydajność – czyli zdolność kolumny do utrzymania wąskiego pasma substancji – jest podstawą teorii półek.
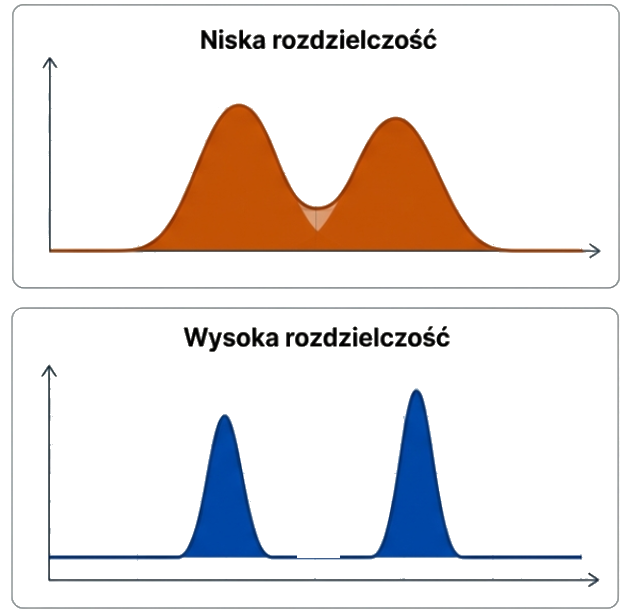
Co to są półki teoretyczne?
Kiedy słyszymy o „półkach” wewnątrz kolumny, intuicja podpowiada nam fizyczne stopnie lub przegrody. Nic bardziej mylnego. Półka teoretyczna to matematyczna abstrakcja.
Wyobraźmy sobie, że proces chromatograficzny to seria następujących po sobie dyskretnych etapów ekstrakcji. Cząsteczka substancji wchodzi w kontakt z fazą stacjonarną, ustala się stan równowagi, po czym faza ruchoma przesuwa ją o krok dalej do kolejnego „mikro-etapu”. Im więcej takich kroków (półek) uda nam się „upchnąć” w kolumnie, tym lepszy będzie rozdział.
Kluczowa myśl: Półka teoretyczna to najmniejszy odcinek kolumny, na którym ustala się stan równowagi termodynamicznej między fazą ruchomą a stacjonarną.
Dziedzictwo Martina i Synge’a: Model Destylacyjny
W 1941 roku Archer Martin i Richard Synge (późniejsi nobliści) zaproponowali model oparty na procesie destylacji frakcjonowanej. W tamtym czasie destylacja była najlepiej opisanym procesem rozdzielczym, a kolumny destylacyjne faktycznie posiadały fizyczne półki.
Martin i Synge spróbowali opisać zachowanie kolumny chromatograficznej tak jakby była kolumną do destylacji. W takim modelu substancja porusza się w dół kolumny w serii skokowych kroków.
Na każdej „półce” faza ruchoma i stacjonarna są w idealnej równowadze.
Choć model ten był genialny w swojej prostocie, miał jedną ogromną wadę: był statyczny. Zakładał, że równowaga ustala się natychmiastowo, co w rzeczywistym przepływie cieczy lub gazu jest niemożliwe.
Wydajność kolumny: Parametry N i H
Aby opisać wydajność kolumny, używamy dwóch kluczowych parametrów:
Liczba półek teoretycznych (N)
Im wyższa wartość N, tym kolumna jest sprawniejsza, a piki węższe. Obliczamy ją z chromatogramu na podstawie czasu retencji (tR) i szerokości piku (w):
Jak łatwo zauważyć liczba półek teoretycznych będzie charakterystyczna dla konkretnej substancji i warunków rozdziału, a nawet dla konkretnego aparatu. Dlatego ważne jest by wyznaczać ją zawsze w takich samych warunkach.

Wysokość równoważna półce teoretycznej (H lub HETP)
To parametr, który mówi nam, jak „gruba” jest jedna półka. Skoro kolumna ma określoną długość (L), to zależność jest prosta:
Analityczny cel: Chcemy, aby H było jak najmniejsze. Niska wartość H oznacza, że na każdym centymetrze kolumny mieści się więcej półek, co przekłada się na wyższą sprawność.
Równanie Van Deemtera, czyli jak sterować wydajnością
W 1956 roku holenderski inżynier Jan van Deemter i jego współpracownicy zauważyli, że model statyczny to za mało. W rzeczywistości cząsteczki analitu nie czekają grzecznie na ustalenie równowagi – one są w ciągłym ruchu, dyfundują i zderzają się z elementami wypełnienia.
Ich Kinetyczna Teoria Rozdziału, opisana jest równaniem:
Gdzie u to prędkość liniowa fazy ruchomej. Równanie opisuje zależność pomiędzy prędkością przepływu a wydajnością kolumny. Oprócz przepływu, można jednak na nim zauważyć trzy składowe, które są ściśle związane z budową kolumny. Te trzy składowe to trzy różne dyfuzje zachodzące w trakcie rozdziału.
Składowe Równania:
- Człon A (Dyfuzja wirowa / Eddy diffusion): Wynika z faktu, że cząsteczki mogą wybierać różne drogi między ziarnami wypełnienia. Jedne płyną „autostradą”, inne kluczą bocznymi uliczkami.
- Jak go zminimalizować? Używając mniejszego i bardziej jednorodnego ziarna wypełnienia. Krótko mówiąc, człon A jest charakterystyczny dla danej kolumny. By go zmniejszyć należy użyć kolumny o niższej ziarnistości lub kolumny z ziarnem typu Core-shield.
- Człon B (Dyfuzja podłużna): Cząsteczki naturalnie chcą się rozprzestrzeniać z miejsc o wysokim stężeniu do niskiego (wzdłuż kolumny). Ten efekt dominuje przy niskich przepływach.
- Człon C (Opory przenoszenia masy): Cząsteczka potrzebuje czasu, aby wejść do fazy stacjonarnej i z niej wyjść. Przy wysokich przepływach faza ruchoma „ucieka” zbyt szybko, zanim cząsteczki zdążą wymienić się między fazami.
Optymalizacja rozdziału w Praktyce
Wykres zależności H od prędkości przepływu to tzw. krzywa van Deemter’a. Zrozumienie krzywej van Deemter’a to klucz do bycia mistrzem optymalizacji.
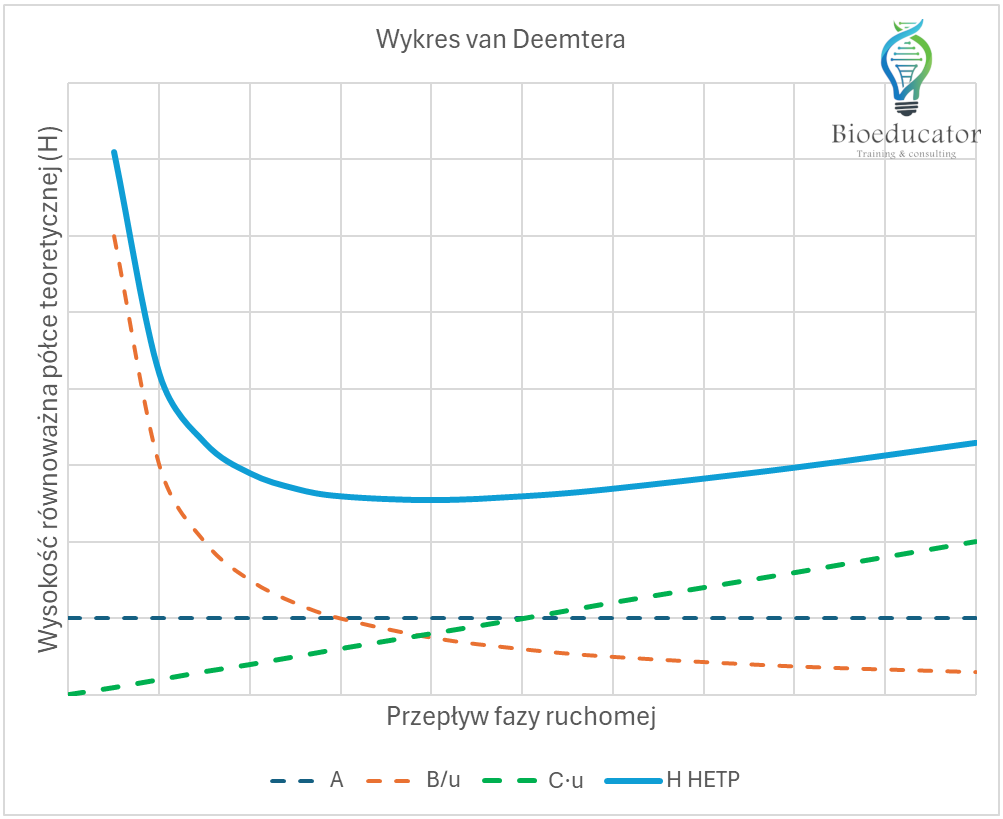
Szukanie Minimum
Krzywa H = f(u) ma kształt litery „U”. Istnieje optymalna prędkość przepływu (uopt), przy której wartość H jest najniższa (czyli sprawność kolumny najwyższa). Pracując przy tej prędkości, uzyskujemy najlepszy możliwy rozdział dla danej kolumny.
GC vs LC: Wielka Bitwa Dyfuzji
W chromatografii gazowej (GC) dyfuzja cząsteczek w fazie ruchomej (gazie) jest tysiące razy szybsza niż w cieczy.
- W GC człon B (dyfuzja podłużna) jest bardzo istotny.
- W chromatografii cieczowej (LC) to człon C (przenoszenie masy) jest głównym hamulcowym. Dlatego w nowoczesnej technice UHPLC (lub UPLC) stosuje się ekstremalnie małe ziarna (poniżej 2 μm), aby skrócić drogę dyfuzji i „spłaszczyć” krzywą Van Deemtera, pozwalając na bardzo szybkie przepływy bez utraty sprawności.
Monitoring żywotności kolumny
W miarę użytkowania możliwości rozdzielcze kolumny spadają. Warto to monitorować a półki teoretyczne idealnie się do tego nadają. Poniższy wykres przedstawia zależność pomiędzy liczbą półek teoretycznych a ilością wykonanych analiz na kolumnie. Monitorując ten parametr można przewidzieć zużycie kolumny i wymienić ją w odpowiednim momencie.
Podsumowanie: Złoty Środek
Teoria półek i równanie Van Deemtera to nie tylko matematyczne ciekawostki. To fundamenty, które pozwalają nam zrozumieć, że:
- Dłuższa kolumna nie zawsze jest rozwiązaniem (bo rośnie czas i ciśnienie).
- Szybszy przepływ oszczędza czas, ale może zrujnować rozdzielczość (przez człon C).
- Mniejsze ziarno wypełnienia to niemal zawsze lepsza sprawność (poprawa członów A i C).
Jako analitycy zawsze szukamy kompromisu między jakością (wysokie N, niskie H) a ekonomią czasu. Dzięki Van Deemterowi wiemy dokładnie, gdzie ten kompromis się znajduje.
